ORPO: Monolithic Preference Optimization without Reference Model (Paper Explained)

1. Alignment enhances model outputs to match desired criteria.

🥈89 03:05

Alignment in ORPO focuses on improving model outputs to align with preferred responses, increasing the likelihood of desired answers and decreasing undesired ones.

• Alignment aims to make model outputs more consistent with expected responses.
• The process involves adjusting model outputs based on preference ratings.
• ORPO ensures that model responses are in line with user expectations.

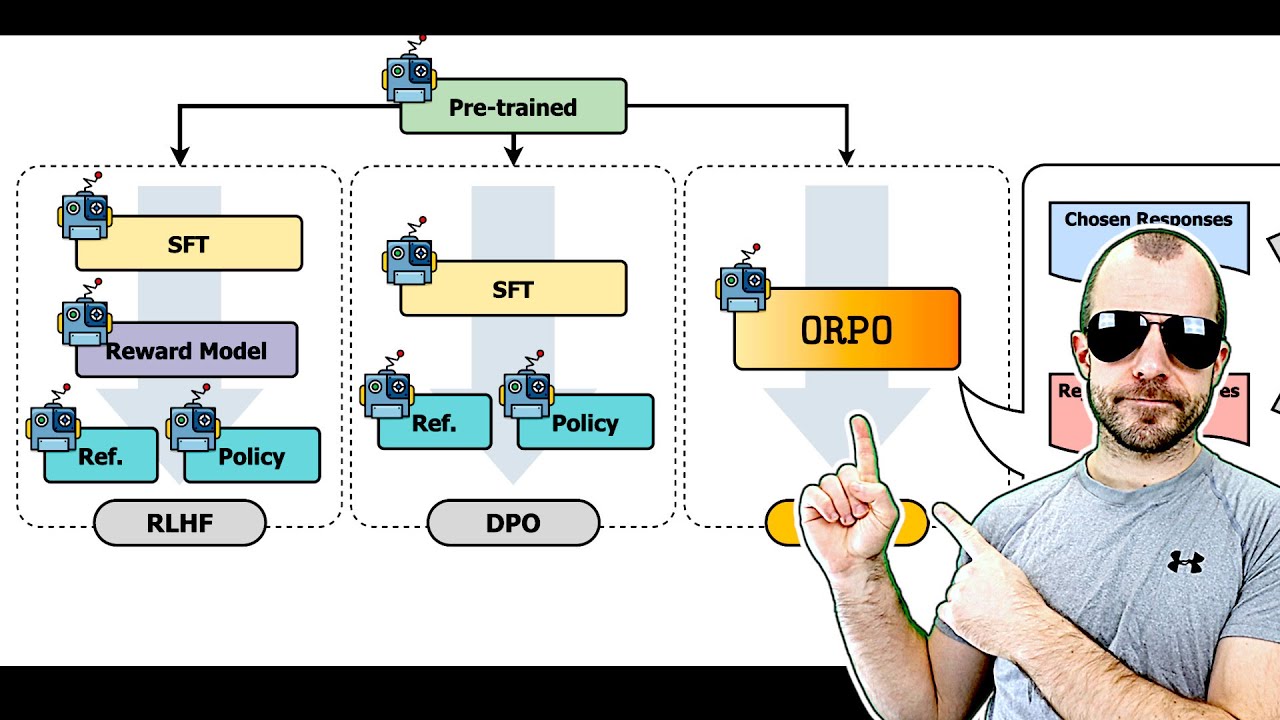
2. ORPO simplifies preference optimization by integrating steps.

🥇92 06:12

ORPO streamlines the process by combining supervised fine-tuning and alignment steps into one procedure, eliminating the need for multiple models and reducing computational requirements.

• ORPO merges supervised fine-tuning and alignment into a unified approach.
• This integration reduces the complexity of the optimization process.
• By combining steps, ORPO enhances efficiency and computational resource utilization.

3. ORPO addresses limitations of supervised fine-tuning for alignment.

🥈87 17:43

ORPO overcomes the shortcomings of supervised fine-tuning by introducing an auxiliary loss to differentiate between desired and undesired model outputs.

• The method corrects the failure of supervised fine-tuning to distinguish between preferred and non-preferred responses.
• By incorporating an auxiliary loss, ORPO ensures better alignment of model outputs.
• The approach enhances the ability to train models to produce desired responses effectively.

4. ORPO's odds ratio loss integrates preference data for alignment.

🥈88 18:10

ORPO utilizes an odds ratio loss that incorporates preference data to guide model training towards generating responses aligned with user preferences.

• The odds ratio loss considers the likelihood of desired responses given specific inputs.
• By leveraging preference data, ORPO optimizes model outputs to match user expectations.
• The odds ratio loss mechanism enhances the alignment process in ORPO.

5. Understanding odds and odds ratio is crucial for modeling.

🥇92 18:27

Odds indicate the likelihood of an event happening compared to not happening, while the odds ratio compares odds between two outcomes.

• Odds show how much more likely an event is to happen than not.
• Odds ratio is the ratio of odds between two outcomes, aiding in comparing probabilities.

6. Logarithmic transformations play a key role in loss functions.

🥈88 20:01

Taking the log of odds ratios and applying non-linearities helps in transforming probabilities for effective modeling.

• Log transformations help in converting values into different spaces for better analysis.
• Non-linearities aid in mapping probabilities to desired ranges for optimization.

7. Weighted contrast gradients enhance model adaptation.

🥈87 26:14

Introducing weighted contrast gradients based on likelihood amplifies model adaptation towards chosen responses, improving alignment.

• Amplifying gradients for low likelihood responses accelerates model adaptation towards desired outputs.
• Balancing gradients based on likelihood enhances model performance and alignment.

8. Preferential use of odds ratio over probability ratios for balanced distributions.

🥈89 30:59

Utilizing odds ratio over probability ratios provides a wider range of values for modeling, ensuring a more balanced and stable distribution.

• Odds ratio offers a more evenly distributed set of values for effective modeling.
• Probability ratios tend to create spiky distributions, limiting modeling flexibility.